Difference between revisions of "Geogebra Clix C01"
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Working with the application=== | ===Working with the application=== | ||
| Line 16: | Line 8: | ||
====Using the tool bar to draw an angle ==== | ====Using the tool bar to draw an angle ==== | ||
In this section you will be introduced to the basic constructions available on the tool bar. | In this section you will be introduced to the basic constructions available on the tool bar. | ||
| − | + | <gallery mode="packed" heights="250px" caption="Introduction to the tool bar"> 2 | |
| − | <gallery mode="packed" heights="250px" caption="Introduction to the tool bar"> | ||
File:Geogebra3.png|Moving objects | File:Geogebra3.png|Moving objects | ||
File:Geogebra4.png|Moving by rotating around a point | File:Geogebra4.png|Moving by rotating around a point | ||
| Line 35: | Line 26: | ||
#Drawing multiple lines: Multiple lines can also be drawn in Geogebra. Parallel lines, perpendicular lines, angle bisectors and perpendicular bisectors can be drawn. | #Drawing multiple lines: Multiple lines can also be drawn in Geogebra. Parallel lines, perpendicular lines, angle bisectors and perpendicular bisectors can be drawn. | ||
| − | ==== | + | ====Measuring an angle==== |
| − | <gallery mode="packed" heights="250px" caption=" | + | <gallery mode="packed" heights="250px" caption="Measuring an angle"> |
| − | File: | + | File:Geogebra_angle_measurement.png |
| − | + | File:Geogebra angle measure.png | |
| − | |||
| − | |||
| − | |||
| − | File:Geogebra | ||
| − | |||
| − | |||
</gallery> | </gallery> | ||
| − | The above set of images show how to | + | |
| − | + | The above set of images show how to measure angles in Geogebra. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====Using the input bar==== | ====Using the input bar==== | ||
Revision as of 23:29, 16 April 2018
Working with the application
Getting familiar with the Geogebra interface
The above image shows you the Geogebra window. After opening Geogebra, you will see the application window as above. The user can define the graphics view in terms of the axes, the grid, scale of the axes, etc. The Move button - which allows objects to be moved is highlighted in blue.
Using the tool bar to draw an angle
In this section you will be introduced to the basic constructions available on the tool bar.
- Introduction to the tool bar
- 2
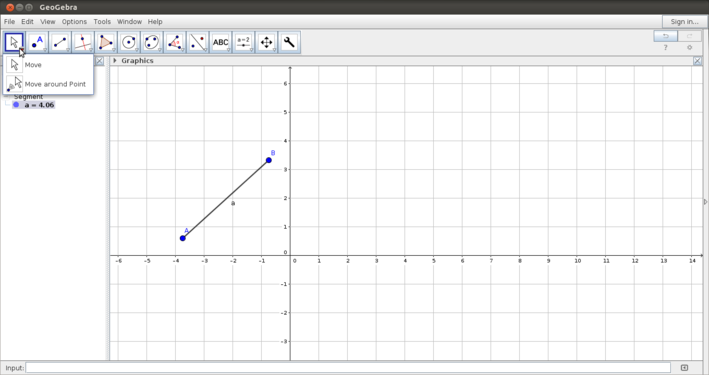
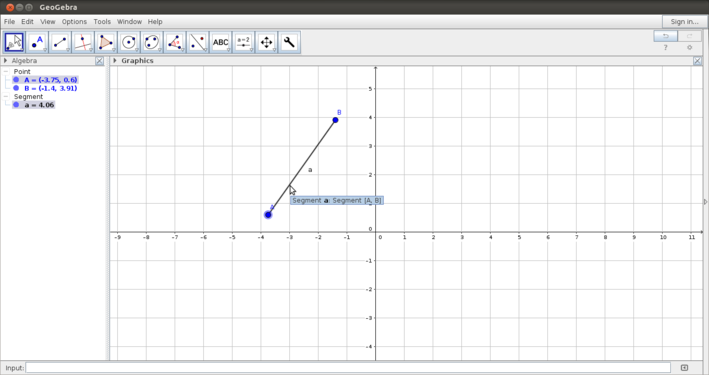
The Geogebra tool bar is very versatile - the construction follows the processes that we would normally follow in paper and pen construction. Some six important categories in the tool bar are discussed below:
- Moving objects:Geogebra allows you to move object constructed freely by dragging the object. You can also select an object and move it by rotating aroung a point.
- Plotting points: There are different ways of plotting points on the Geogebra graphics pad. You can plot a point anywhere on the graphics view - this is a free point. You can also plot on an object or as an intersection of two objects; in both the cases the point is a dependent object.
- Drawing lines: The menu for lines and segments also allows multiple constructions - segments,lines, rays and vectors
- Drawing multiple lines: Multiple lines can also be drawn in Geogebra. Parallel lines, perpendicular lines, angle bisectors and perpendicular bisectors can be drawn.
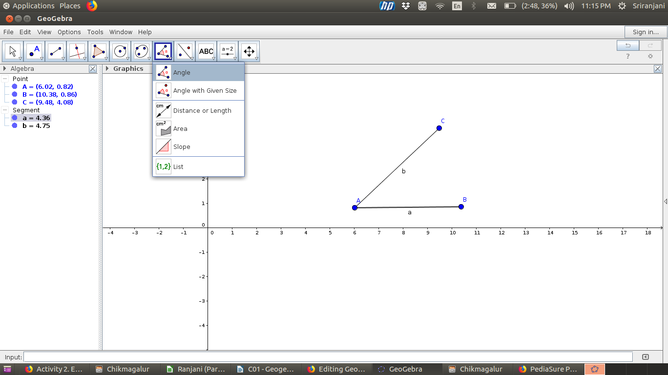
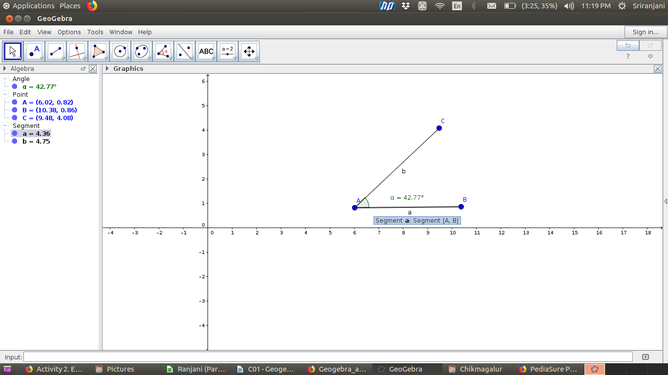
Measuring an angle
- Measuring an angle
The above set of images show how to measure angles in Geogebra.
Using the input bar
- Using the input bar
In Geogebra, all the constructions you can do using the tool bar can also be done with definitions on the input bar. The input bar also follows the same mathematical conventions used in the tool bar.
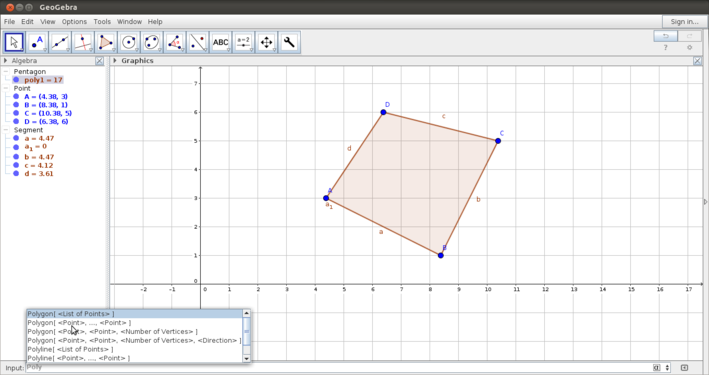
- Input bar for sketches: The first image shows defining polygon with a set of points
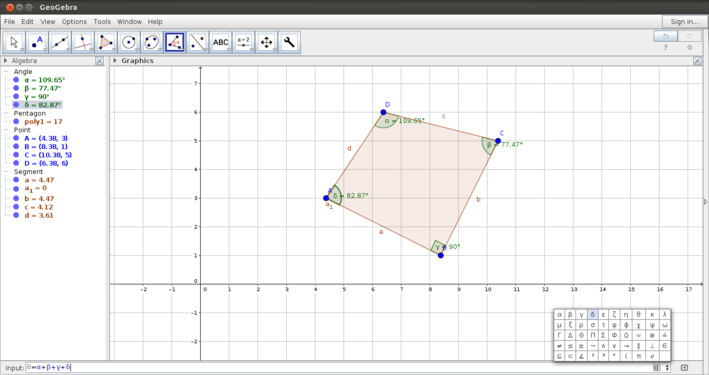
- Input bar for calculations: The second image shows how to use the input bar for defining variables and values for parameters. You can also use this space as a calculator for values and properties being shown in the construction. In this image the angle sum of the quadrilateral is being calculated in the input bar.
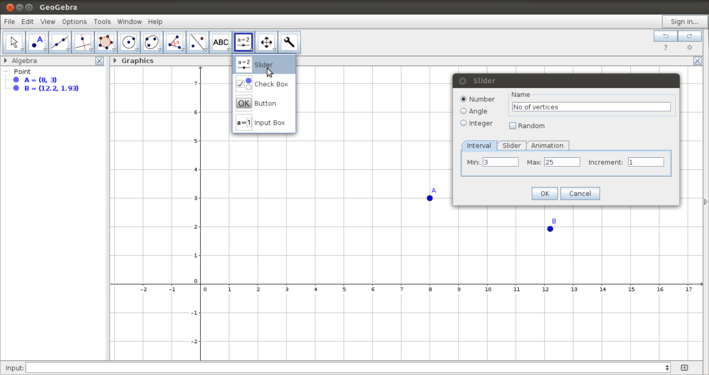
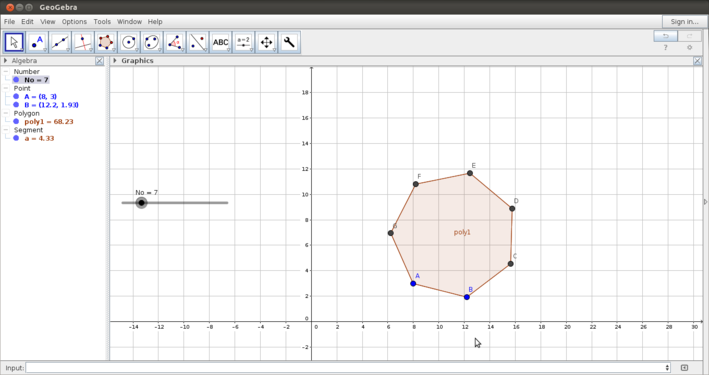
Using the tool bar - slider
One of the powerful features of Geogebra is the dynamic feature. You can vary parameters of the shape that you want to animate and see how properties change.
- Using the slider
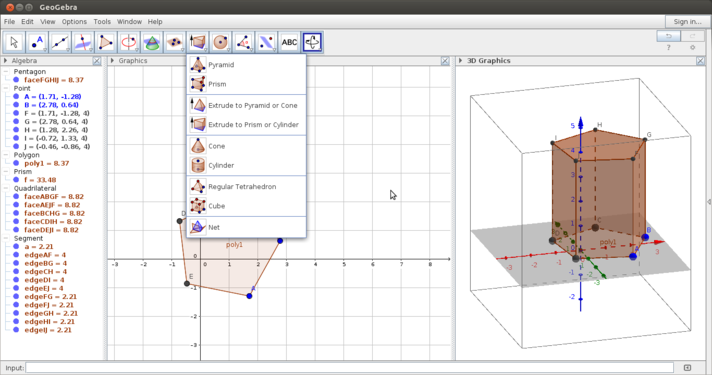
3D view
- Using the 3D window
- The 3D window allows you to visualize the geometry along 3-axes. You can rotate the graphics view using the same icon that you used for the Move graphics view. You can independently work on the 2D and 3D windows and the construction on one window will get reflected in the other.
- The 3D window allows you to construct solid figures by extruding from a 2-dimensional shapes. Other features include construction of a plane, rotation, reflection., etc. The slider defined in the 2D window will help animate in the 3D window also.
Using Geogebra to make a given sketch
You have learnt many functionalities. An example of how to use these different tools to create a Geogebra construction can be found here.
Saving and exporting
- You can save Geogebra file from the File menu.
- You can also export the Geogebra file as an image (.png format) or as an animated graphic (.gif format).
- If you export the Geogebra file as html you can publish it on the repository for Geogebra files.
Advanced features
- Creating your own tool in Geogebra
- Making three dimensional animations
- Exporting Geogebra pages as html to add to the repository of Geogebra materials
Ideas for resource creation
- Geogebra sketches for demonstrating different problems in geometry
- Geogebra can be combined with screencast recording to create a video recording of a lesson with a Geogebra file; this can be used for students' self learning as well.
References
|}